基于 Diffusion Model 的文本到音乐生成

基于 Diffusion Model 的文本到音乐生成#

虽然我们可以用整个教程来讨论 diffusion（扩散）在生成式音频中的工作原理（事实上，今年在 ISMIR 上已有人做了这样的教程！），但这里我们先简要回顾 diffusion 的工作原理，然后介绍如何将文本条件融入这些模型，并以 Stable Audio Open 作为案例研究。

Diffusion：通过迭代精炼实现连续值生成#

../_images/diff1.png

Fig. 4 与操作离散 token 的语言模型不同，我们应该如何设计模型来生成连续数据？#

与基于语言模型的方法生成离散 token \(x \in \mathbb{N}\) 不同，diffusion 的目标是生成某些连续值数据 \(x \in \mathbb{R}\)（这与更经典的 VAE 和 GAN 模型相同）。

形式化地说，如果我们的数据来自某个分布 \(\mathbf{x} \sim p(\mathbf{x})\)，那么目标是学习某个模型，使我们能够从该分布中采样 \(p_\theta(\mathbf{x}) \approx p(\mathbf{x})\)。实际上，为了从数据分布中采样，在 VAE/GAN 中我们将模型参数化为某个生成器 \(G_\theta\)，使得：

\[ \mathbf{x} = G_\theta(z), \quad z \sim \mathcal{N}(0, \boldsymbol{I}), \]

即我们学习某个模型，将各向同性的高斯噪声转换为我们的目标数据。

Diffusion model 在许多生成式媒体任务上比这些经典模型更成功 [DN21]（也更具可控性）的主要原因之一是其迭代精炼的能力。在上面的方程中，整个生成过程发生在单次模型调用中。虽然这当然是高效的（许多 diffusion model 在概念上重新发明了 GAN 以利用其效率 [KLL+23, NZC+24]），但在单次模型前向传播中要完成的工作量非常大，尤其是对于高维数据！

如果我们能在一次模型调用中只生成 \(\mathbf{x}\) 的一部分，那将非常有用。这样，我们就可以多次调用模型来完整生成 \(\mathbf{x}\)（如果你注意到了，这听起来与自回归非常相似）。

为了构建这种”多步生成器”，我们首先需要引入将数据腐蚀为噪声的概念（注意：虽然这一步在我们精简的 diffusion 介绍中不太容易融入，但我们鼓励读者查阅更完整的 diffusion 资料，它们从更宽泛的视角来阐述这个范式 [SSDK+21]）。首先，我们调整符号以建模从干净数据到噪声的扩散过程，用时间步 \(0\rightarrow T\) 表示，其中 \(\mathbf{x}_0 \sim p_0(\mathbf{x}_0)\) 是我们的干净数据（即之前的 \(\mathbf{x} \sim p(\mathbf{x})\)），\(\mathbf{x}_T \sim p_T(\mathbf{x}_T)\) 是纯高斯噪声（即之前的 \(z\)）。然后，我们可以定义一个扩散过程，通过随机微分方程（SDE）逐步将干净数据 \(\mathbf{x}_0\) 转变为高斯噪声 \(\mathbf{x}_T\)：

\[ \mathrm{d}\mathbf{x} = f(\mathbf{x}, t)\mathrm{d}t + g(t)\mathrm{d}\boldsymbol{w}, \]

其中 \(\boldsymbol{w}\) 是标准维纳过程（即加性高斯噪声），\(f(\mathbf{x}, t)\) 是 \(\mathbf{x}_t\) 的漂移系数，\(g(t)\) 是扩散系数。如果 SDE 看起来难以理解，需要记住的关键点是：上述方程定义了一个 \(0\rightarrow T\) 的过程，逐渐向数据添加噪声，直到只剩下噪声。为了清晰起见，我们用 \(p_t(\mathbf{x})\) 表示 \(\mathbf{x}_t\) 的边际概率密度。

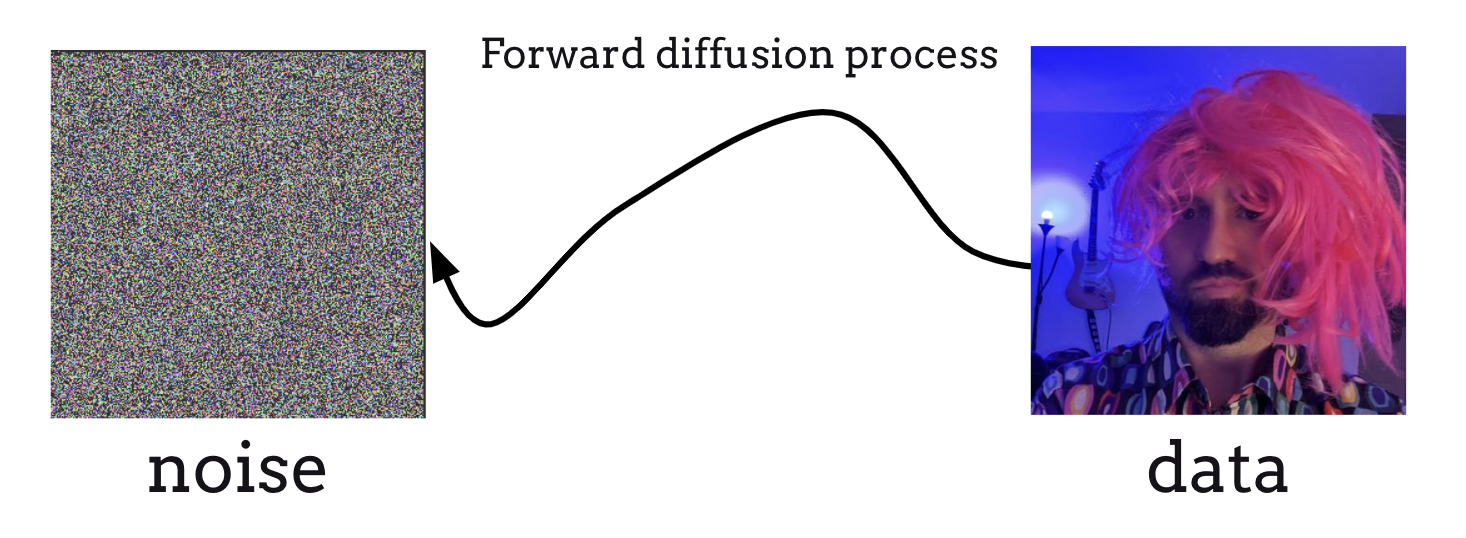
../_images/diff2.png

Fig. 5 Diffusion model 的起点是定义一个前向加噪过程，逐步将我们的数据腐蚀为高斯噪声。#

这之所以重要，是因为 [And82] 的一个巧妙结果允许我们定义一个将高斯噪声转换回数据的逆向扩散过程，由以下公式给出：

\[ \mathrm{d}\mathbf{x} = [f(\mathbf{x}, t) - g(t)^2\nabla_{\mathbf{x}}\log p_t(\mathbf{x})]\mathrm{d}t + g(t)\mathrm{d}\bar{\boldsymbol{w}}, \]

其中 \(\bar{\boldsymbol{w}}\) 是逆时间维纳过程，值得注意的是，\(\nabla_{\mathbf{x}}\log p_t(\mathbf{x})\) 是 \(\mathbf{x}_t\) 边际概率分布的得分函数（score function）。通俗地说，得分函数定义了一个指向数据分布中更高密度区域的方向，你可以想象它类似于获取一维曲线路径的导数，只不过是在高维空间中。

由于我们现在有了定义从噪声到数据的过程的方法，可以看出 VAE/GAN 本质上是在学习一个积分上述逆时间 SDE（从 \(T\) 到 \(0\)）的生成器，从而学习从噪声到数据的直接映射。 然而，diffusion model 的优势在于学习一个得分模型 \(s_\theta(\mathbf{x}, t) \approx \nabla_{\mathbf{x}}\log p_t(\mathbf{x})\)。通过这种方式，diffusion model 分多步迭代求解逆时间 SDE，在某种意义上以固定步长沿着逆扩散路径前进，在每个点检查导数以确定下一步应该走向哪里。这样，diffusion model 能够迭代地精炼模型输出，从起始的各向同性高斯噪声中逐步去除越来越多的噪声，直到我们的数据变得清晰！

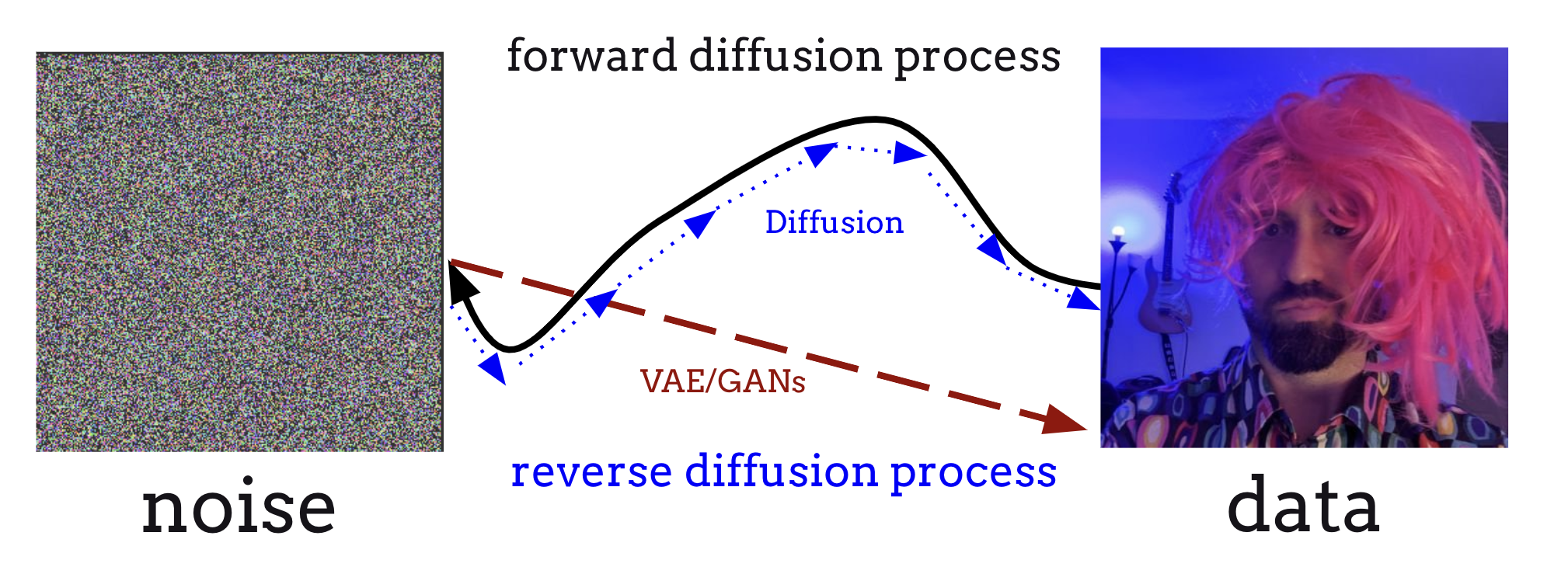
../_images/diff3.png

Fig. 6 VAE/GAN 建模的是从噪声到数据的直接映射，而 diffusion model 建模的是逆扩散过程的得分，这使得我们可以使用任何现成的 SDE 求解器沿逆扩散路径生成数据。#

如果这一切听起来像是语言模型进行自回归的某种奇特版本，那你的想法大致是对的！Sander Dieleman 有一篇精彩的博客文章讨论了这种概念上的相似性，以及如何将 diffusion 想象为在频谱域中的自回归。

以上就是我们对 diffusion model 的介绍。虽然这里有很多数学内容，但只要你理解核心思想——diffusion model 近似的是从噪声到数据路径的梯度（而非学习路径本身）——你就可以顺利继续本教程了！

表示方法#

与自回归语言模型方法不同，自2021年 diffusion 出现以来，基于 diffusion 的文本到音乐（TTM）生成的具体输入表示方法变化很大。下面我们按大致时间顺序列出：

  1. 直接波形建模：\(\mathbf{x}_0 \in \mathbb{R}^{f_s T \times 1}\)，其中 \(f_s\) 是音频的采样率，\(T\) 是总时长（秒）。换言之，我们直接在原始音频信号上执行扩散过程。这种输入表示通常不被使用，原因既包括原始音频信号的规模可能非常大（仅30秒的 44.1 kHz 音频就超过100万个浮点数！），也因为 diffusion 在原始音频信号上效果不佳（而且有充分的理由解释这一点）。

  2. 直接（梅尔）频谱图建模 [NMBKB24a, WDWB23, ZWCD23]：\(\mathbf{x}_0 \in \mathbb{R}^{H \times W \times C}\)，其中 \(H\) 和 \(W\) 是音频（梅尔）频谱图的高度和宽度，\(C\) 是通道数（通常为1，但使用复数频谱图时可以为2）。这样，TTM diffusion 的过程几乎与非潜在空间的图像 diffusion 完全相同，因为我们只是将音频频谱图视为”图像”并在这些二维信号上运行 diffusion。由于我们不能直接将梅尔频谱图转换回音频，这些模型通常训练 [ZCDB24] 或使用现成的 [WDWB23] 声码器 \(V(\mathbf{x}_0) : \mathbb{R}^{H \times W \times C} \rightarrow \mathbb{R}^{f_s T \times 1}\) 将生成的梅尔频谱图转换回音频。

  3. 潜在（梅尔）频谱图建模 [CWL+24, FM22, LCY+23a, LYL+24]：\(\mathbf{x}_0 \in \mathbb{R}^{D_h \times D_w \times D_c}\)，其中 \(D_h, D_w, D_c\) 是频谱图通过二维自编码器后的潜在高度、宽度和通道数（通常 \(D_h \ll H, D_w \ll W\) 以提高效率，而 \(D_c > C\)）。这可能是真正开创 TTM 生成领域的第一个设计，[FM22] 使用现有的 Stable Diffusion 自编码器并在频谱图上微调 SD。因此，这需要在训练 TTM diffusion 模型之前单独训练一个 VAE \(\mathcal{D}, \mathcal{E}\)。训练完成后，从模型采样包括用 diffusion 生成潜在表示，将其通过解码器 \(\mathcal{D}(\mathbf{x}_0): \mathbb{R}^{D_h \times D_w \times D_c} \rightarrow \mathbb{R}^{H \times W \times C}\)，然后将该输出通过声码器 \(V\)。

  4. DAC 风格的潜在音频建模 [ECT+24, EPC+24, NZC+24]：\(\mathbf{x}_0 \in \mathbb{R}^{D_T \times 1 \times D_c}\)，其中 \(D_T\) 是压缩音频信号的长度，因为这里我们绕过了声码器和频谱图 VAE，而是使用原始音频 VAE 将音频直接压缩为潜在的一维（但多通道，因为 \(D_c\) 通常为 32/64/96）序列。实际上，这与 Encodec [DCSA22] 或 DAC [KSL+23] 等离散语言模型编解码器几乎完全相同，唯一的区别是离散向量量化被替换为标准的 VAE KL 正则化，从而给出连续值潜在表示而非离散 token。事实上，训练过程和架构的其余部分基本保持不变（即全卷积一维编码器/解码器配合 snake 激活函数、多分辨率 STFT 判别器等）。因此，从模型采样时，我们生成潜在表示并直接通过解码器 \(\mathcal{D}\) 获取音频输出。在本教程的后续部分，我们将重点关注这种方法，因为它是 Stable Audio Open 所使用的。

架构#

在架构设计方面，大多数 diffusion model 遵循两大类之一：U-Net 和 Diffusion Transformer (DiT)。在本文中，我们重点关注 DiT，原因既包括大多数现代 diffusion model 正在采用这种建模范式 [ECT+24, EPC+24, NZC+24]，也因为 DiT 在代码设计上简单得多。一个 TTM DiT 通常看起来大致如下：

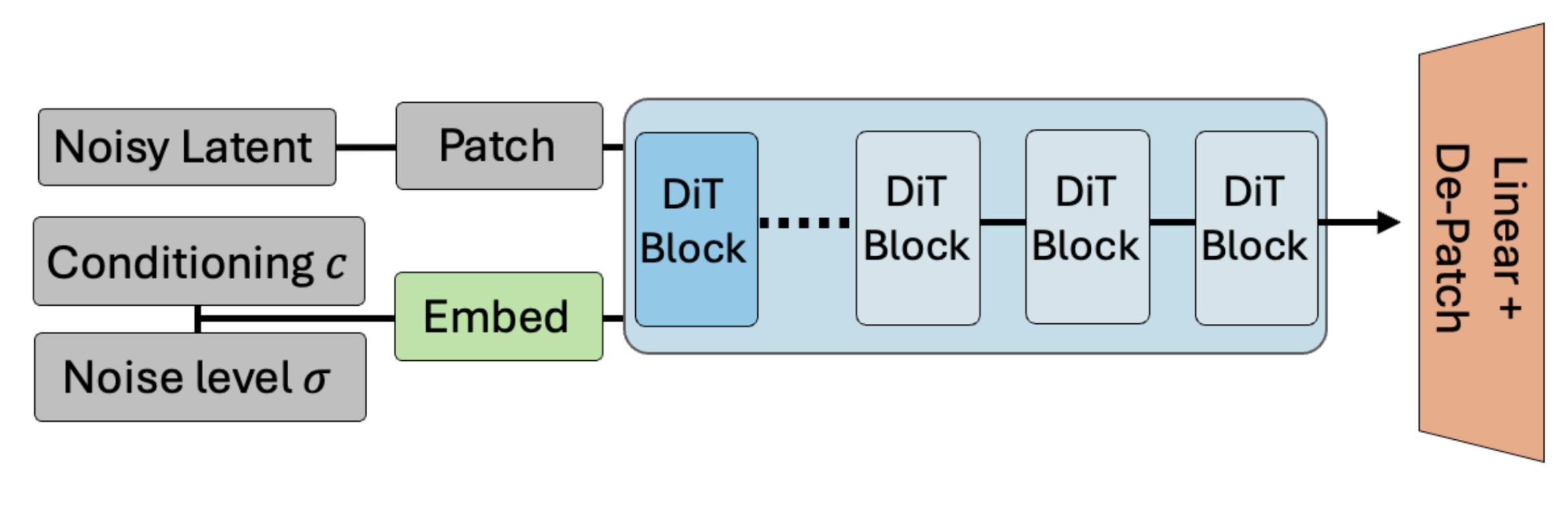
../_images/dit.png

Fig. 7 DiT 包含一个用于噪声输入数据的初始分块（patchify）和嵌入层，以及噪声级别和条件的嵌入，然后将其通过一系列双向 Transformer 模块（其中条件信息会调制噪声潜在表示的内部表征），最后投影回去以预测干净的潜在表示。#

具体来说，在输入的潜在表示被转换为”分块”（即进一步下采样）并且输入条件（即文本，稍后详细介绍）和时间步/噪声级别被转换为相应的嵌入之后，DiT 只是一系列操作在此潜在表示上的双向 Transformer 编码器模块（类似 BERT）（条件信息提供某种形式的调制），最后通过线性层和反分块层得到我们的预测。相比 U-Net，DiT 具有许多良好的扩展特性，能够更好地处理可变长度序列，并且由于没有手动的残差下采样/上采样模块，代码明显更简洁。

条件机制#

现在最大的问题是，文本条件在模型中究竟是如何发挥作用的？在进入模型之前，文本提示 \(\mathbf{c}_{\textrm{text}}\) 首先需要从字符串转换为某种数值嵌入，我们将其称为 \(\mathbf{e}_{\textrm{text}} = \textrm{Emb}(\mathbf{c}_{\textrm{text}})\)，其中 \(\textrm{Emb}\) 是某个嵌入提取函数。在许多情况下，\(\textrm{Emb}\) 使用预训练的文本骨干网络（如 CLAP 或 T5），然后通过一个或多个线性层将嵌入投影到正确的尺寸。嵌入后，\(\mathbf{e}_{\textrm{text}}\) 要么是全局嵌入 \(\mathbb{R}^{d}\)，要么是序列级嵌入 \(\mathbb{R}^{d \times \ell}\)，其中 \(d\) 是 DiT 的隐藏维度，\(\ell\) 表示文本嵌入的 token 长度（即文本嵌入可以按 token 提取，T5 就是这种情况）。

现在 \(\mathbf{e}_{\textrm{text}}\) 可以通过多种方式与模型内部的主扩散潜在表示交互（这些方式可以组合使用），下面我们介绍其中几种：

  1. 时域拼接（又称上下文内条件或前缀条件）：这里，我们简单地将文本条件附加到扩散潜在序列中，得到新的潜在表示 \(\hat{\mathbf{x}} = [\mathbf{x}, \mathbf{e}_{\textrm{text}}] \in \mathbb{R}^{(D_T + \ell) \times 1 \times d}\)，其中 \([\cdot]\) 是沿时间轴的拼接操作（即序列变长），并在所有 DiT 模块之后移除这些额外的 token。这样，文本仅通过 DiT 的自注意力模块作用于扩散潜在表示，根据文本嵌入的长度会导致最小到中等程度的速度下降。

  2. 通道拼接：这里，\(\mathbf{e}_{\textrm{text}}\) 首先被投影为与主扩散潜在表示相同的序列长度，然后沿通道维度拼接 \(\hat{\mathbf{x}} = [\mathbf{x}, \textrm{Proj}(\mathbf{e}_{\textrm{text}})] \in \mathbb{R}^{(D_T) \times 1 \times 2d}\)（即序列在某种意义上变得更深）。这种方法通常不太用于文本条件（但对其他条件效果很好），因为它赋予文本一种时间性，而全局描述并不具备这种特征。

  3. Cross-Attention（交叉注意力）：这里，我们在每个 DiT 模块的自注意力层之间添加额外的交叉注意力层，扩散潜在表示直接关注 \(\mathbf{e}_{\textrm{text}}\)。这可能提供最佳的控制能力（也是 Stable Audio Open 所使用的方法），代价是由于每个交叉注意力层的二次计算成本而增加了最多的计算量。

  4. Adaptive Layer-Norm (AdaLN，自适应层归一化)：这里，每个 DiT 模块中的层归一化通过从 \(\mathbf{e}_{\textrm{text}}\) 学习的偏移、缩放和门控参数（隐藏维度每个索引各一个）来增强，这些参数通过一个小型 MLP 学习得到：\(\gamma_{\textrm{shift}}, \gamma_{\textrm{scale}}, \gamma_{\textrm{gate}} = \textrm{MLP}(\mathbf{e}_{\textrm{text}})\)。这为模型增加的计算量最少，也是原始 DiT 工作所使用的方法 [PX23]。值得注意的是，从本质上讲，这与 MusicLDM [CWL+24] 中使用的 Feature-wise Linear Modulation (FiLM) 层几乎完全相同。这些偏移、缩放和门控参数还可以被零初始化，使得每个模块本质上被初始化为恒等函数，这就是”AdaLN-Zero”所指的含义。

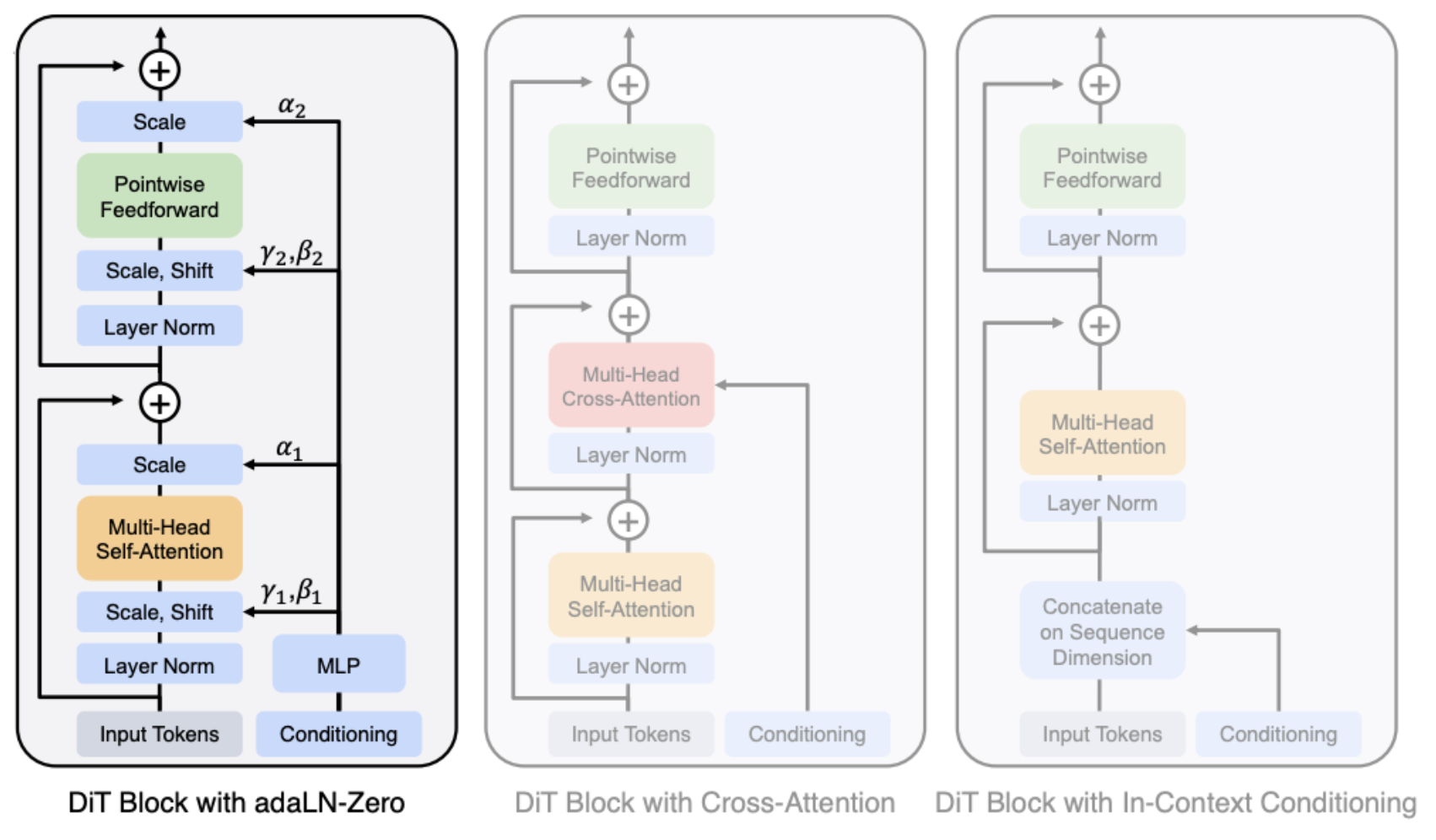
../_images/conds.png

Fig. 8 DiT 可以通过多种方式进行条件化，包括自适应层归一化、交叉注意力和上下文内条件（时域拼接）。#

Contents